To novices in Deep Learning, figuring out the dimension of a convolutional network and the number of learnable parameters in it could be itimidating at first. This is largely due to the confusing usage of jargons (like depth, filter and fiber) and the parameters sharing scheme. This artile will focus on introduction of the structure of a common ConvNet and clarify and compare a few of them that are used for describing the dimensionality of ConvNet.

A basic ConvNet may be comprised of three layers: an INPUT Layer, a CONV Layer (with activation), POOL layer and a Fully-Connected layer. Since activation is required for every convolutional layer, it is not considered a seperate layer here. The input layer is often an image.

INPUT Layer

The dimension of input volume is determined by the size and channels of the image. For example, if we have an image with a resolution of 32\(\times\)32 and 3 channels, then the input volume size should be 32\(\times\)32\(\times\)3.

lowercase input layer in following part means "last layer"

CONV Layer

Neurons in CONV layer is arranged in 3 dimensions which could be discribed by length, width and depth. Each neuron connects to only a subset of neurons (local connectivity) taken from a 2-d square area called "receptive field" in input layer. The size of receptive field is defined by its side length \(F\). Since neurons in input layer is also 3-d, whether it is a CONV layer or an INPUT layer, the number of weights for a single neuron here is \(F\times F\times {d}_{-1}\) in which \({d}_{-1}\) is the depth of input layer. \(F\) is a hyperparameter which is non-learnable and should be set manually.

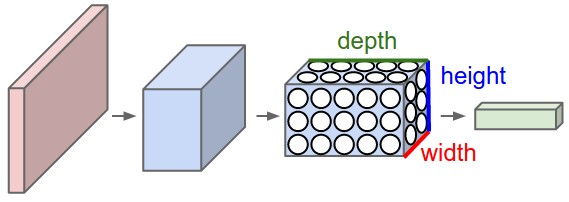
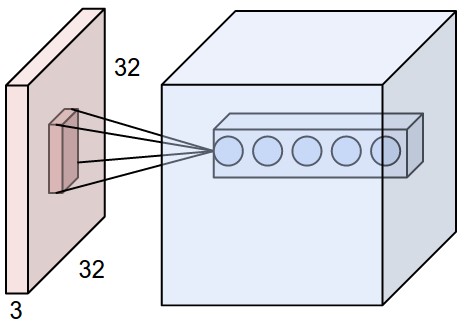
The receptive field of neighboring neurons should cover slightly different areas, the difference is called Stride (\(S\)). When iterating over neurons of a depth slice, the receptive field is moving across input layer (side length \(W\)) with step of \(S\). So the number of neurons needed to cover input layer spatial size is \({((W-F)/S+1)}^2\), often denoted by \((W-F)/S+1\) for brevity. In this way, the side length of CONV layer will be smaller than input layer. But it's usually preferable to use zero padding to retain spatial dimentionality. If the input layer is zero padded by an amount of \(P\), the size of a depth slice of neurons will be \((W−F+2P)/S+1\).

At the core of a Convolution layer is the parameter sharing scheme, each neuron in the same depth slice share the same sets of weights. So the forward pass of the CONV layer can in each depth slice be computed as a convolution of the neuron’s weights with the input volume, hence the name convolutional neural network. The weights work like a filter over an image, so it is often referd as filter or kernel.

The total number of neurons in a CONV layer is \({((W-F)/S+1)}^2*d\), where \(d\) is the depth of neurons. And \(d\) is a hyperparameter and is set to increase in consecutive CONV layers. Since neurons in the same depth slice share the same set of weights, number of weights to train for the all neurons in the layer is \(F\times F\times {d}_{-1} \times d\). The number of parameters to train is \(F\times F\times {d}_{-1} \times d + d\), acounting for the bias.

POOL layer

Pooling, often max pooling, is used to reduce the number of parameters. Pooling works also works like a filter, with side length of \(F\) and stride of \(S\), the side length of neurons in POOL layer is \({((W-F)/S+1)}^2\). The depth \(d\) is usually set to be equal to input layer. Total number of neurons in Poolin layer is \({((W-F)/S+1)}^2 \times d\). The number of parameters to train is \(F\times F\times {d}_{-1} \times d + d\), acounting for the bias.

Output Layer

The number of neurons is the same as its input layer (denoted as \(C\)). The number of parameters will be \(C\times(C+1)\), since it is a fully-connected layer, which is a lot larger than contingent CONV layer.